ساخت هوش مصنوعی ساده با پایتون: قسمت سوم، آموزش شبکه‌های عصبی

رضا دهقان

۲۹ آبان ۱۴۰۲

تکنولوژی ، مقالات

مدت مطالعه: ۴ دقیقه

تعداد بازدید‌: ۶۸۶

هوش مصنوعی

در پست قبلی دیدیم که شبکه عصبی ما توانست یک خروجی را درست پیش‌بینی کند و برای پیش‌بینی دوم دچار خطا شد. اگر پست‌های قبلی را هنوز نخوانده‌اید، قبل از شروع این پست به سراغ آن‌ها بروید.

در این پست قصد داریم شبکه عصبی خودمان را آموزش دهیم تا پیش‌بینی‌های دقیق‌تری انجام دهد. در فرایند آموزش شبکه‌های عصبی شما ابتدا باید خطا را ارزیابی کرده و سپس وزن را مطابق با آن تغییر دهید. برای تنظیم وزن‌ها، ما از الگوریتم‌های کاهش گرادیان و پس‌انتشار استفاده می‌کنیم. اما قبل از انجام هرگونه تغییر، ابتدا باید خطار را اندازه‌گیری کنیم.

ساخت هوش مصنوعی ساده با پایتون: قسمت اول، مفاهیم و اصول اولیه شبکه‌های عصبی

محاسبه خطای پیش‌بینی

شما برای درک اندازه خطا به راهی برای اندازه گیری آن نیاز دارید. تابعی که برای این کار استفاده می شود، تابع هزینه نام دارد. در این مثال ما از میانگین توان دوم خطاها (یا mean squared error) به عنوان تابع هزینه استفاده می‌کنیم. این میانگین در دو مرحله محاسبه می‌شود:

محاسبه اختلاف بین مقدار پیش‌بینی و مقدار هدف
ضرب نتیجه در خودش

از آن‌جایی که ما مجذور اختلاف بین پیش‌بینی و هدف را داریم، نتیجه همیشه مثبت خواهد بود. کد زیر برای محاسبه این مقدار استفاده می‌شود:

In &#091;24]: target = 0

In &#091;25]: mse = np.square(prediction - target)

In &#091;26]: print(f"Prediction: {prediction}; Error: {mse}")
Out&#091;26]: Prediction: &#091;0.87101915]; Error: &#091;0.7586743596667225]

In &#۰۹۱;۲۴]: target = 0

In &#۰۹۱;۲۵]: mse = np.square(prediction - target)

In &#۰۹۱;۲۶]: print(f"Prediction: {prediction}; Error: {mse}")

Out&#۰۹۱;۲۶]: Prediction: [0.87101915]; Error: [0.7586743596667225]

مشاهده می‌کنید که مقدار خطا معادل ۰/۷۵ محاسبه شده است.

درک نحوه کاهش خطا

در این قسمت هدف شما تغییر وزن‌ها و بایاس است تا مقدار خطا کم شود. برای درک بهتر این فرایند، ما تنها وزن‌ها را تغییر می‌دهیم و بایاس را ثابت نگه می‌داریم. همچنین می‌توانیم تابع سیگموید را نیز حذف کرده و تنها از نتیجه layer_1 استفاده کنیم. حالا فقط باید وزن‌ها را طوری تغییر دهیم تا مقدار کاهش پیدا کند.

برای محاسبه MSE (توان دوم خطاها) از دستور (error = np.square(prediction – target استفاده می‌کنیم. اگر مقدار (prediction – target) را به عنوان یک متغیر ثابت با نام x در نظر بگیریم، دستور ما به (error = np.square(x تبدیل می‌شود که یک تابع مربعی است. نمودار این تابع به شکل زیر است:

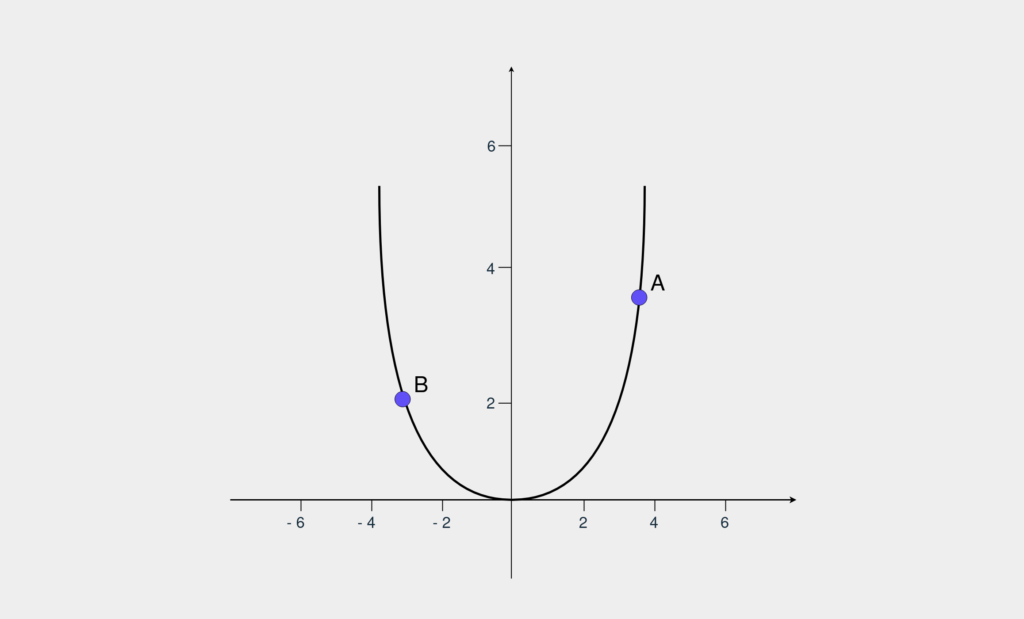
مقدار خطا با محور y نشان داده می‌شود. اگر شما در نقطه A هستید و می‌خواهید خطا را به صفر برسانید، باید مقدار x را کاهش دهید. در سوی دیگر اگر در نقطه B باشید، باید مقدار x را افزایش دهید. برای تشخیص جهت حرکت برای کاهش خطا، از مشتق استفاده می‌کنیم. اگر از زمان ریاضی دبیرستان و دانشگاه یادتان نیست، مشتق به ما نشان می‌دهد یک الگو چطور تغییر می‌کند. گرادیان نام دیگر مشتق است و الگوریتم کاهش گرادیان برای تشخیص جهت حرکت به کار می‌رود.

با یک محاسبه ساده متوجه می‌شویم که مشتق (np.square(x برابر با ۲x و مشتق x برابر با یک است. اگر مقدار مشتق به دست‌آمده برابر مثبت باشد پیش‌بینی شما بالا بوده و باید وزن را کاهش دهید و اگر منفی باشد، برعکس. کد این فرایند را در زیر می‌بینید:

In &#091;27]: derivative = 2 * (prediction - target)

In &#091;28]: print(f"The derivative is {derivative}")
Out&#091;28]: The derivative is: &#091;1.7420383]

In &#۰۹۱;۲۷]: derivative = 2 * (prediction - target)

In &#۰۹۱;۲۸]: print(f"The derivative is {derivative}")

Out&#۰۹۱;۲۸]: The derivative is: [1.7420383]

نتیجه به دست‌آمده ۱/۷۴ است و بنابراین باید وزن را کاهش دهیم. برای این کار مقدار مشتق را از بردار وزن کم می‌کنیم. حالا مقدار weights_1 را با توجه به نتیجه به دست آمده عوض می‌کنیم و دوباره پیش‌بینی را انجام می‌دهیم:

In &#091;29]: # Updating the weights
In &#091;30]: weights_1 = weights_1 - derivative

In &#091;31]: prediction = make_prediction(input_vector, weights_1, bias)

In &#091;32]: error = (prediction - target) ** 2

In &#091;33]: print(f"Prediction: {prediction}; Error: {error}")
Out&#091;33]: Prediction: &#091;0.01496248]; Error: &#091;0.00022388]

In &#۰۹۱;۲۹]: # Updating the weights

In &#۰۹۱;۳۰]: weights_1 = weights_1 - derivative

In &#۰۹۱;۳۱]: prediction = make_prediction(input_vector, weights_1, bias)

In &#۰۹۱;۳۲]: error = (prediction - target) ** 2

In &#۰۹۱;۳۳]: print(f"Prediction: {prediction}; Error: {error}")

Out&#۰۹۱;۳۳]: Prediction: [0.01496248]; Error: [0.00022388]

می‌بینید مقدار خطا نزدیک به ۰ شده است. در این مثال مقدار مشتق کوچک بود، اما در برخی موارد مقدار مشتق بسیار بزرگ است. برای مثال در نمودار بالا افزایش‌های بالا مناسب نیستند چرا که ممکن است به طور مستقیم از نقطه A به نقطه B رفته و به ۰ نزدیک نشویم. برای جبران این موضوع، وزن‌ها را به اندازه بخشی از مقدار مشتق تغییر می‌دهیم و برای تعیین مقدار این بخش، از پارامتر آلفا یا نرخ یادگیری بهره می‌بریم. اگر نرخ یادگیری را کاهش دهید، مقدار افزیش‌ها نیز کوچک می‌شود. اما از کجا بدانیم بهترین نرخ یادگیری چقدر است؟ با حدس و تکرار.

نکته: به طور معمول مقادیر نرخ یادگیری برابر با ۰/۱، ۰/۰۱ یا ۰/۰۰۱ است.

ساخت هوش مصنوعی ساده با پایتون: قسمت دوم، توسعه مدل شبکه عصبی

پیاده‌سازی قانون زنجیر

در شبکه عصبی باید بردارهای وزن و بایاس را با هم تغییر دهیم. تابعی که برای اندازه‌گیری خطا استفاده می‌کنید به هر دو متغیر وزن و بایاس بستگی دارد. از آن‌جایی که متغیرهای وزن و بایاس مستقل هستند، می‌توانید آن‌ها را به دلخواه تغییر دهید تا نتیجه دلخواه به‌دست آید.

شبکه عصبی ما دو لایه دارد، و از آن‌جایی که هر لایه حاوی توابع خاص خود است، شما با یک ترکیب تابع سروکار دارید. این یعنی مقدار x در تابع خطای (np.square(x خود نتیجه یک تابع دیگر است.

حالا برای محاسبه مشتق خطای پارامترها، از قانون زنجیر در محاسبات استفاده می‌کنیم.

با استفاده از این قانون شما مشتق جزیی هر تابع را اندازه‌گیری کرده و همه را در هم ضرب می‌کنید تا به مشتق مورد نظر خود برسید.

تصویر زیر فرایند این کار را نشان می‌دهد:

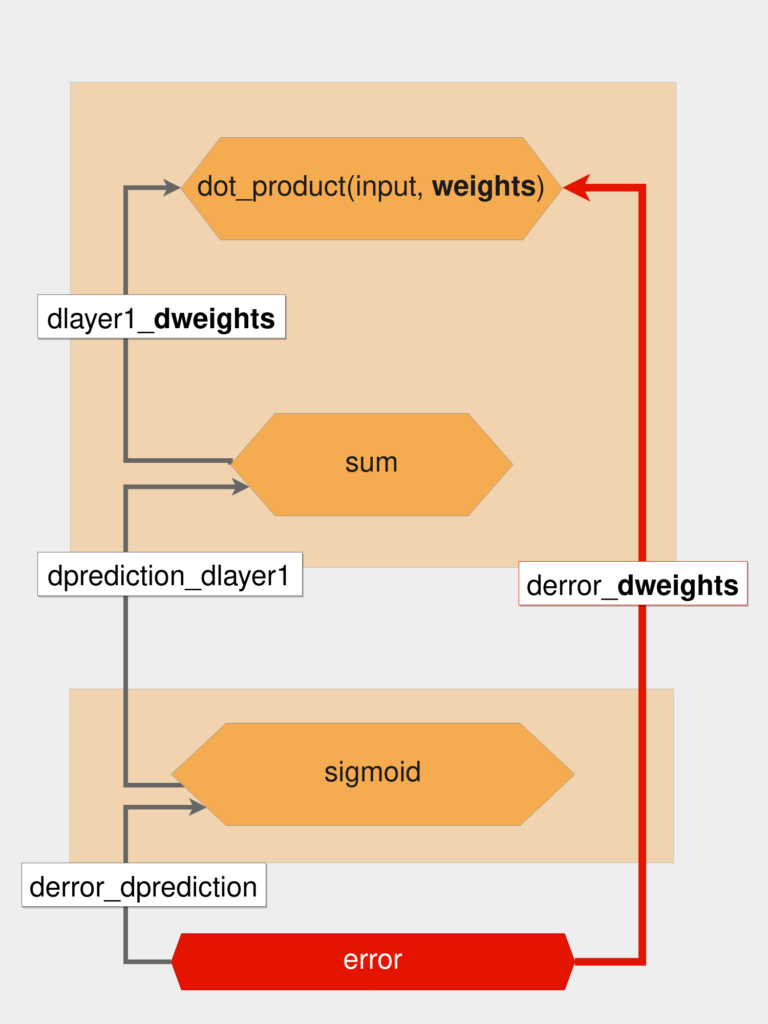
با توجه به تصویر بالا و قانون زنجیر، مقدار derror_dweights به صورت زیر محاسبه می‌شود:

derror_dweights = (
&nbsp; &nbsp; derror_dprediction * dprediction_dlayer1 * dlayer1_dweights
)

derror_dweights = (

    derror_dprediction * dprediction_dlayer1 * dlayer1_dweights

)

این فرایند «گرفتن مشتق جزیی، اندازه‌گیری و ضرب» قانون زنجیر است و الگوریتمی که برای به‌روزرسانی پارامترهای شبکه عصبی استفاده می‌کنیم الگوریتم پس‌انتشار نام دارد. در قسمت بعدی پارامترها را با استفاده از پس‌انتشار تنظیم کرده و کلاس شبکه‌های عصبی خودمان را می‌سازیم.